Casio FC-200V Manual - User Manual

Download PDF User Manual

Full Text Searchable PDF User Manual

Casio Financial Consultant

A Supplementary Reader - Part 2

An Electronic Publication
By QED Education Scientific

Contents

QED Education Scientific

CASIO Financial Consultant:
A Supplementary Reader - Part 2

CONTENTS

Page

Introduction

Compound Interest with CMPD

Doing Amortization with AMRT

FC-200V & FC-100V Comparison Chart

Introduction

QED Education Scientific

INTRODUCTION

Welcome to the world of

CASIO Financial Consultant

calculator.

The intention of this 4-part reader is to supplement the User’s Guide of FC-
100V/FC-200V. We adopt the work-example approach as we believe this makes the
reader both effective and efficient for use. Some examples are slightly methodical,
but you should find them useful nonetheless. The goals of the 4 parts are:

Part 1 – Help users get started and explore the interface and setting.

Part 2 – Using CMPD and AMRT for loan and annuity related calculations.

Part 3 – Help users get familiar with CASH and CNVR modes.

Part 4 – Using FC-200V Bond and Depreciation calculations

The FC-200V is an extended version of the FC-100V, and for your convenience we
include a comparison chart of both models in the reader. Key-strokes for all financial
modes for both models are cleverly remained the same by

CASIO

, with the

exception  to  Bond,  Depreciation  and  Break-Even  Value,  which  are  functions  only
available  on  the  FC-200V.  User  will  also  find  that  operations  of  some  scientific
calculations are different too. We refer ONLY to FC-200V in all examples but owner
of FC-100V will find that the examples provided also work on their machine.

We  have  referred  to  these  resources  for  inspiration:  (i)  Schaum’s  Outlines  on
Mathematics of  Finance  and  (ii)  Casio’s  Financial  Activity  for TVM.  Screenshots  in
the  pages  are  screen  dumps  from  the  Casio  AFX-2.0+.  For  this  we  would  like  to
thank Marco Corporation (M) Sdn. Bhd. for their technical support.

We did our best to reduce number of mistakes within this reader. But if you do see
any, you are most welcome to report them via

info@qed-edu.com

. Please also send

us your feedbacks.

Mun Chou, Fong

Product Specialist
QED Education Scientific Sdn. Bhd.

First publication: June 2006, Edition 1
This publication: June 2007, Edition 2

All Rights Reserved. Permission to print, store or transmit is hereby given to reader for personal use. However, no part of
this booklet may be reproduced, store or transmitted in any form by any means for commercial purposes without prior
notice to QED Education Scientific Sdn. Bhd.

This publication makes reference to the Casio FC-200V and FC-100V Financial Consultants. These model descriptions are
the registered trademark of Casio Computer Inc.

Compound Interest with CMPD

QED Education Scientific

CMPD

EXE

SETUP

EXE

CMPD

EXE

(

─

)

EXE

SOLVE

Compound Interest with CMPD

The  enhanced  display  screen  and  apparent  interactivity  of  the  FC  100V/200V
actually  makes  calculation  such  as  compound  interest  calculation  much  easier.  In
our  discussion  we  calculate  partial  month  using  compound  interest,  and  we  use

(compounded

times a year) to represent the nominal interest rates.

Example 1

►

Enter CMPD mode and set partial month calculation to CI.

Operation

Enter CMPD mode by tapping on

, then tap on

. If [dn:CI] is displayed,

let it be. Otherwise, scroll down and set it to ‘CI’.

So we have set partial month calculation as [dn:CI].

█

Example 2

►

Find the compound interest on $1,000 for 2 years at 12%

compounded semi-annually, or

In CMPD mode, n is the number of compound periods, P/Y is the number of annual payment, while
C/Y is the number of annual compounding. Check page E-45 of the User Guide.

Operation

As interest is compounded twice a year, the number of compound periods is n = 2x2
= 4. Also, interest is paid twice a year, so we have P/Y = 2. Lastly, C/Y is the
number of annual compounding, so C/Y is 2.

Enter CMPD mode and make sure the calculator displays [Set:End]. Scroll down,

enter 2 for [n], 12 for [

], (-)1000 for [PV], 0 for [PMT], 1 for [P/Y] and 2 for [C/Y].

Scroll up to select [FV] and solve it.

So the future value (sum of principal and accumulated interest) is approximately
$1262.48. Obviously the compound interest is $1262.48 - $1000 = $262.48.

█

Output: FV = 1262.47696

Screenshot from Casio TVM

Compound Interest with CMPD

QED Education Scientific

EXE

CMPD

EXE

(

─

)

EXE

SOLVE

•

EXE

CMPD

EXE

(

─

)

EXE

•

EXE

Example 3

►

Find the monthly installment of a 25-year, $100,000 mortgage

loan at interest of 6.25% compounded monthly.

In this example, n = 25x12 = 300,

% = 6.25, PV = 100,000, P/Y (installment paid monthly) = C/Y = 12.

Operation

Enter CMPD mode. The calculator should display [Set:End] since payment is

made at the end of each period. Enter 25x12 for [n], 6.25 for [

], (-)100,000 for

[PV], 12 for [P/Y] and 12 for [C/Y].

Scroll up to select [PMT] and solve it.

Therefore the monthly installment of the mortgage loan is about $659.70.

Suppose the mortgage loan above is calculated based on daily interest, so to find
the monthly repayment, we set [C/Y] as 365 and then solve for [PMT] again.

█

The CMPD mode also enables user to find other parameters such as interest rate.

Example 4

►

The earning per share of common stock of a company increased

from $4.85 to $9.12 for the last 5 years. Find the compounded annual rate of
increase.

In this example, n = 5, PV = -4.85 (payment made earlier), FV = 9.12, while P/Y = C/Y = 1. All other
parameters = 0.

Operation

Enter CMPD mode, ensure that [Set:End] is displayed. Enter 5 for [n], -4.85 for

[PV], 9.12 for [FV] and 1 for both [P/Y] and [C/Y].

Output: PMT = 659.6693783

Screenshot from Casio TVM

Compound Interest with CMPD

QED Education Scientific

SOLVE

EXE

CMPD

EXE

SOLVE

•

EXE

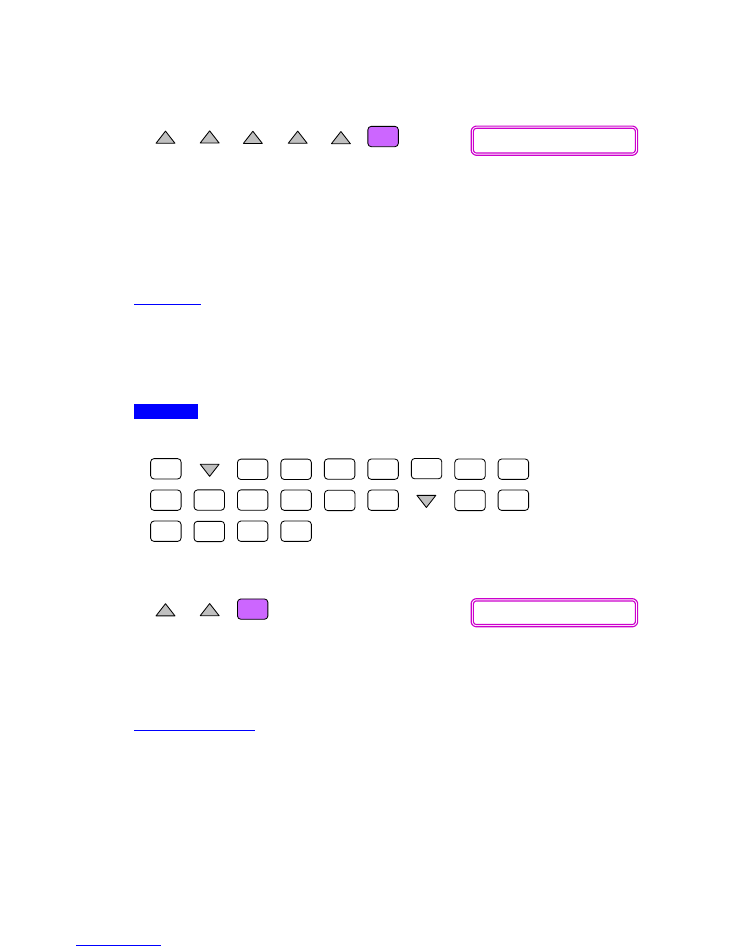
Now scroll up to select [

] and solve it.

Therefore the compounded annual increase rate of this stock for the last 5 years is
about 13.46%.

█

The previous example shows that when sufficient information is provided, we could
calculate for most parameters available in CMPD mode. The next example is simple
annuity calculation made possible with the CMPD mode of FC-100V/FC-200V.

Example 5

►

My friend JT was repaying a debt with payments of $250 a

month. He misses his payments for November, December, January and February.
What payment will be required in March to put him back on schedule, if interest is at

In this example, Set = End, n = 5 (months),

% = 14.4, PMT = 250, P/Y = C/Y = 12. Other parameters

= 0.

Operation

Once entered CMPD mode, make sure that [Set:End] is shown. Enter 5 for [n],

14.4 for [

], 0 for [PV], 250 for [PMT], 12 for both [P/Y] and [C/Y].

Scroll up to select [FV] and solve it.

Hence JT needs to settle $1280.36 in March to get back on the loan repayment
schedule.

█

For Understanding

►

A company estimates that a machine will need to be

replaced 10 years from now at a cost of $350,000. How much must be set aside
each year to provide that money if the company’s savings earn interest at

Answer: $23977.37

Output:

% = 13.46204842

Output: FV = -1280.362165

Doing Amortization with AMRT

QED Education Scientific

EXE

CMPD

EXE

(

─

)

EXE

SOLVE

AMRT

EXE

SOLVE

Doing Amortization with AMRT

The AMRT mode of 100V/200V allows user to perform amortization, which shares
many parameters/variables with the CMPD mode. In examples that follow we shall
be able to see the advantage of such ‘sharing’. Note that some amortization
problems are actually simple annuity problems which we can solve using the CMPD
mode (refer to Example 5 of

Compound Interest with CMPD

This first  example finds  the  outstanding balance of a  loan  after  certain numbers  of
payment are made.

Example 1

►

A loan of $5,000 is to be amortized with equal monthly payment

over 2 years at

. Find the outstanding principal (balance) after 8 months.

Check page E-55 of the user guide for definitions of PM1, PM2, BAL, INT, PRN,

∑

INT

and

∑

PRN. For

this example, n = 2x12 = 24,

% = 7, PV = -5,000, P/Y = = C/Y = 12. Other parameters = 0.

Operation

As we need to know the monthly payment of the loan, so we begin at CMPD mode.
When monthly payment is found we proceed to AMRT mode for other calculations.

Enter CMPD mode, make sure calculator displays [Set:End]. Scroll down, enter

24 for [n], 7 for [

], (-)5000 for [PV], 0 for [FV], 12 for [P/Y] and [C/Y].

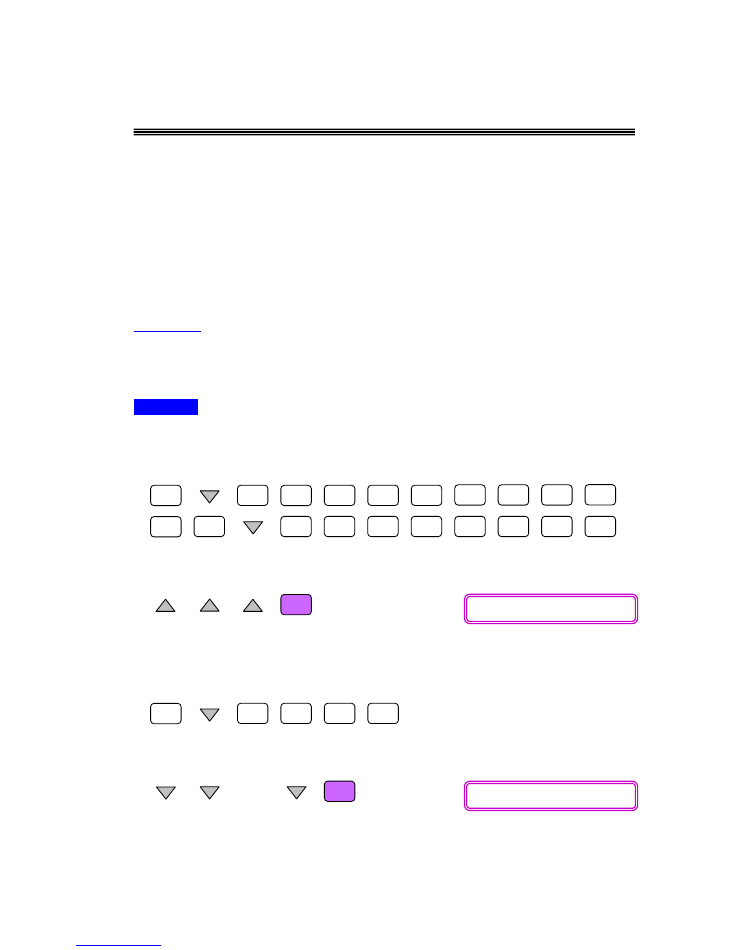
Now scroll up to select [PMT] and solve it.

So the monthly payment for the loan is about $223.86. Now find the outstanding
principal.

Enter AMRT mode, scroll down to enter 1 for [PM1] and 8 for [PM2].

Scroll down further to select [BAL:Solve] and solve it.

Therefore the outstanding balance after 8 payments is approximately $3410.26.

█

Output: PMT = 223.8628955

•

Output: BAL = -3410.256063

Doing Amortization with AMRT

QED Education Scientific

AMRT

EXE

SOLVE

ESC

EXE

CMPD

EXE

(

─

)

EXE

In this last example we could have entered values other than 1 to PM1 and still get
the same result, as long as the values entered are integer

≥

1. However, in most

circumstances we should always let PM1 < PM2 whenever possible (see page E-57
of User Guide.)

Example 2

►

Referring to Example 1, find the interest portion and the principal

portion of the 9

payment.

Operation

If you are doing this immediately after Example 1, then all relevant values are still
intact and you can continue; otherwise you should enter those values again.

Enter AMRT mode, scroll down to enter 9 for [PM1], make sure [PM2] is not = 0.

Scroll down further to select [INT:Solve] and solve it.

Therefore the interest portion of this 9

payment is about $19.90.

Return to AMRT, and then scroll to select [PRN:Solve] and solve it.

The calculator indicates that the principal portion of 9

payment is about $203.97.

█

Example 3

►

Lucas borrows $35,000 at

to buy a car. The loan should

be repaid with monthly installment over three years. Find the total interest paid in
the 12 payments of the second year.

Operation

Again we begin at CMPD mode to find the monthly payment of the loan.

Enter CMPD mode and make sure calculator displays [Set:End]. Then scroll

down and enter 36 for [n], 3 for [

], (-)35000 for [PV], 0 for [FV], 12 for [P/Y] and

[C/Y].

•

Output: INT = 19.89316037

Output: PRN = 203.9697351

Screenshot from Casio TVM

Doing Amortization with AMRT

QED Education Scientific

SOLVE

AMRT

EXE

SOLVE

EXE

CMPD

EXE

(

─

)

EXE

Now scroll up to select [PMT] and solve it.

The monthly payment is about $1017.84. Next, to find the total interest paid in the
second year.

Enter AMRT mode and scroll down to enter 13 for [PM1] and 24 for [PM2].

Scroll down further to select [

∑

INT:Solve] and solve it.

The interest paid in the second year is $550.93.

Note that we entered 13, not 12, for PM1. This is due to the definition of PM1 (see
page E-56 of User Guide.)

█

Interest rate of mortgage tends to change accordingly and this can affect the total
repayment amount, as well as the length of time needed to repay the debt.

Example 4

►

QED Finance issues mortgages where payments are determined

by interest rate that prevails on the day the loan is made. The monthly payments do
not change although the interest rate varies according to market forces. However,
the duration required to repay the loan will change accordingly as a result of this.
Suppose a person takes out a 20-year, $70,000 mortgage at

. After exactly

2 years interest rates change. Find the duration of the loan and the final smaller
payment if the new interest rate stays fixed at

Operation

First we should find the monthly payment of the loan.

Enter CMPD mode, make sure calculator displays [Set:End]. Then scroll down

and enter 240 for [n], 9 for [

], (-)70000 for [PV], 0 for [FV], 12 for [P/Y] and [C/Y].

Output: PMT = 1017.842337

•

Output: ∑INT = 550.9318646

Screenshot from Casio TVM

Doing Amortization with AMRT

QED Education Scientific

SOLVE

AMRT

EXE

SOLVE

CMPD

EXE

SOLVE

Ans

EXE

SOLVE

SHIFT

CTLG

COMP

EXE

SHIFT

CTLG

EXE

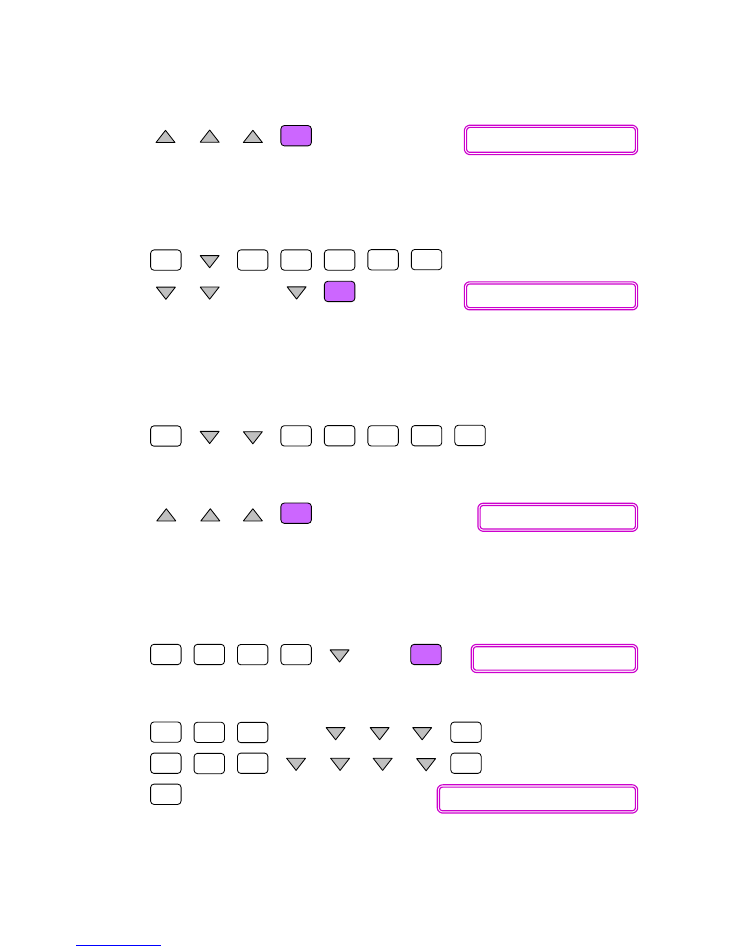
Now scroll up to select [PMT] and solve it.

The monthly repayment amount is $629.81. Next, find the outstanding principal after
2 years.

Enter AMRT mode and scroll down to enter 1 for [PM1] and 24 for [PM2]. Then,

scroll to select [BAL:Solve] and solve it.

The new loan duration will be calculated using this new outstanding balance where
the monthly payment remains at $629.81 but the interest rate is now at

To find the changed loan duration we return to CMPD mode, enter the new

outstanding balance as PV and enter 10 for [

]. Note that the new outstanding

balance is now stored in the Answer Memory.

Once these values are entered, scroll up to select [n] and solve it.

Thus there are 265 more payment of $629.81 plus a final smaller payment. In other
words the new loan duration is 266 months, or total is 24 + 266 = 290 months.
Finally, we find the future value of the repayment with loan duration of 266 months;
the difference between this future value and monthly payment is the final payment.

While in CMPD mode, enter 266 for [n], and scroll down to select [FV] and solve it.

Now calculate PMT + FV (FV is negative) at COMP mode.

Therefore the final, smaller payment is $538.92.

█

Output: PMT = 629.8081691

•

Output: BAL = -67255.23435

Output: n = 265.8551734

Output: FV = -90.88962559

•

(VARS)

Output: PMT + FV = 538.9185435

Doing Amortization with AMRT

QED Education Scientific

EXE

CMPD

EXE

(

─

)

EXE

SOLVE

AMRT

EXE

SOLVE

EXE

CMPD

EXE

(

─

)

•

Often borrower would want to re-finance long term loan. Using CMPD and AMRT in
combination, we can easily compare the cost of re-financing with the savings due to
decide whether the re-financing exercise would be profitable.

Example 5

►

A borrower has an $8,000 loan with QED Finance which is to be

repaid over 4 years at

. In case of early repayment, the borrower is to pay

a penalty of 3 months’ payments. Right after the 20

payment, the borrower

determines that his banker would lend him the money at

. Should he re-

finance?

Operation

First let’s find the monthly payment of the loan.

Enter CMPD mode, make sure calculator displays [Set:End]. Then scroll down

and enter 48 for [n], 18 for [

], (-)8000 for [PV], 0 for [FV], 12 for [P/Y] and [C/Y].

Scroll up to select [PMT] and solve it.

So the monthly payment is about $235 and the outstanding principal after 20
payments would be about $5340.78, as calculated below.

Enter AMRT mode and scroll down to enter 1 for [PM1] and 20 for [PM2]. Then,

scroll to select [BAL:Solve] and solve it.

Thus the total to be refinanced is 5340.78 + 3(235) = $6045.78. Now we can obtain
the new monthly payment at CMPD mode for comparison.

Enter CMPD mode, enter 28 (less 20 months) for [n], 13.5 for [

], (-)6045.78 for

[PV]. Other parameters’ values are retained.

Output: PMT = 234.9999969

•

Output: BAL = -5340.778356

Screenshot from Casio TVM

Doing Amortization with AMRT

QED Education Scientific

SOLVE

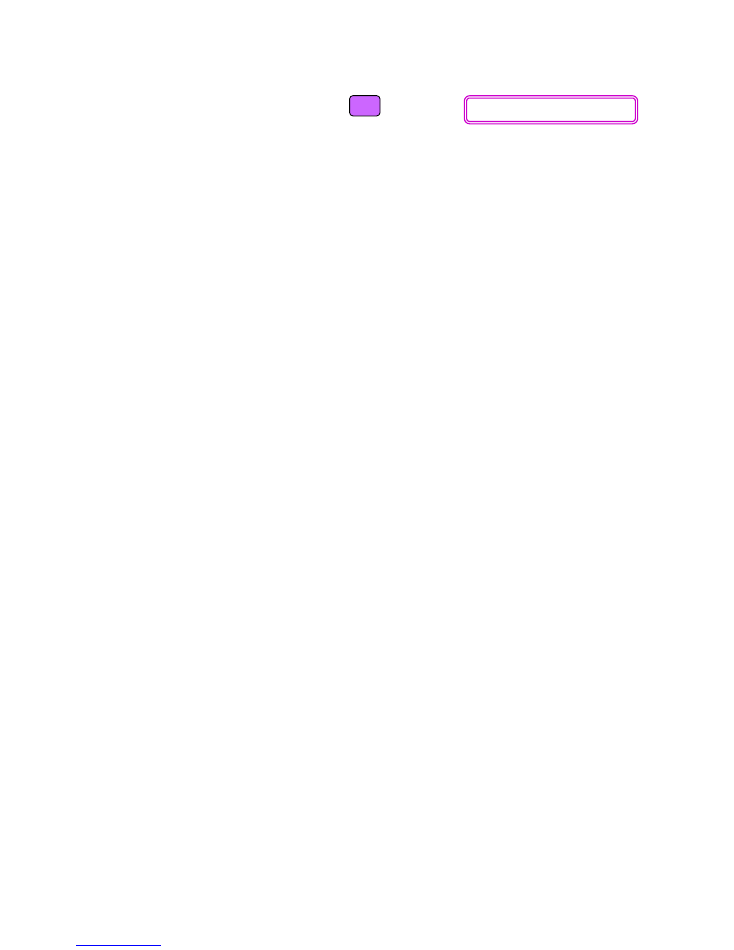
With [PMT] now selected, press

to solve it.

Thus the new monthly payment is $252.91, which exceeds the original monthly
payment of $235. Clearly the re-financing exercise is not profitable.

█

Output: PMT = 252.9130458

Compiled for Marco Corporation. June 2007

FC-200V/FC-100V Comparison Chart

Calculator Functions

FC-200V

FC-100V

Scientific Calculation

Yes

1- & 2- Variable Statistics

Yes

Statistical Regression

Yes

Simple Interest

Yes

Compound Interest

Yes

Cash Flow (IRR, NPV, PBP, NFV)

Yes

Amortization

Yes

Interest Rate Conversion

Yes

Cost & Margin Calculation

Yes

Days and Date Calculation

Yes

Depreciation

Yes

Bonds

Yes

Breakeven Point

Yes

Key Applications

Business and Finance Studies

●

Banking and Banking Studies

●

Insurance and Financial Planning

●

Investment Appraisal

●

Stock Market and Bonds

●

Business and Financial Investment

●

Product Features

Expression Entry Method

Algebraic

Screen Display

4 Lines x 16 Characters

Memory (plus Ans Memory)

Programmable?

Settings and Functions Short Cut Keys

Yes, 2

Function Catalog

Yes

Batteries

Solar Cell & LR44

1 x AAA-Size

Dimension (mm)

12.2 x 80 x 161

13.7 x 80 x 161

Weight

105g

110g